寒假力扣日志

刷题顺序参考如下：https://leetcode-cn.com/circle/article/48kq9d/

目录

链表相关

数组相关

动态规划相关

链表相关

力扣203移除链表元素

难点在于如何处理头节点。解决方法是添加一个哨兵节点(dummy node)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
ListNode* removeElements(ListNode* head, int val) {
       if(!head)return NULL;
       ListNode* newhead = new ListNode();
       newhead->next = head;
       ListNode* pre, *cur;
       pre = newhead;
       cur = head;
       while(cur){
           ListNode* temp = nullptr;
           if(cur->val == val){
               pre->next = cur->next;
                temp = cur;
               cur = cur->next;
               delete temp;
           }
           if(temp)continue;
           cur = cur->next;
           pre = pre->next;
       }
       ListNode* temp = newhead->next;
       delete newhead;
           return temp;
   }

力扣237删除链表中的节点

算法思路

这道题函数中只有一个节点，要求删除该节点。（没有给出头节点）

一道简单的脑筋急转弯。由于题目强调了绝对不会删除掉尾节点，只需把下一个节点的元素赋给node，删除掉下一个节点即可。

代码实现

1
2
3
4
5
6
void deleteNode(ListNode* node) {
        node->val = node->next->val;
        node->next = node->next->next;
        // ListNode* temp = node->next;
        // delete temp;
    }

注意：在实现的过程中还是出现了问题，上面注释掉的代码，为什么不正确？

下面这篇文章讲的很好，c++的指针类型分为静态分配和动态分配。

delete只能用于释放堆指针，也就是new出来的指针，而不能用于栈指针。

如果在deleteNode前在使用c节点本身，那就可能引发不确定行为。

由于ListNode是个单链表节点，而单链表节点本质上是无法做到在链表里删除自身的，所以这题只能通过这种替换的方式来伪造删除了节点。

这题会误导很多开发者，这题的设计模式更是不可取！

个人认为这题应该删除

而203. 移除链表元素这题才是真正的移除链表元素！

作者：AmazingPP 链接：https://leetcode-cn.com/problems/delete-node-in-a-linked-list/solution/tong-pi-ci-ti-li-ying-shan-chu-yin-chu-c-taij/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

力扣19 删除链表的倒数第 N 个结点

算法思路

方法一：暴力法

 1. 遍历一遍，获取链表的长度
 2. 再循环L-n-1次，获取目标结点的前一个结点。

方法二：快慢指针法（只需遍历一遍）

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummynode = new ListNode();
        dummynode->next = head;
        ListNode* fast = dummynode;
        ListNode* slow = dummynode;
        for(int i = 0; i < n; i ++){
            fast = fast->next;
        }
        while(fast->next){
            fast = fast->next;
            slow = slow->next;
        }
        ListNode* temp = slow->next;
        slow->next = slow->next->next;
        delete temp;
        return dummynode->next;
    }

力扣430 扁平化多级双向链表

题目要求

1

变化为

2

算法思路

  1. DFS（事实上，歪着脖子看，就是二叉树的前序遍历）将结点存入数组中
  2. 遍历数组，从新连接结点

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    vector<Node*> arr;
public:
    void dfs(Node* head){
        if(!head)return;
        arr.push_back(head);
        dfs(head->child);
        dfs(head->next);
    }
    Node* flatten(Node* head) {
        dfs(head);
        int size = arr.size();
        for(int i = 0; i < size;  i++){
            if(i+1 < size) arr[i]->next = arr[i+1];
            if(i>0) arr[i]->prev = arr[i-1];
            arr[i]->child = NULL;
        }
        return head;
    }
};

因为前两天学习到很多方法，所以今天的题目都能很快完成

力扣61 旋转链表

力扣24 两两交换链表中的节点

力扣206 反转链表

算法思路

  1. 迭代法（三指针）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    class Solution {
    public:
        ListNode* reverseList(ListNode* head) {
            ListNode* dummynode = new ListNode(0,head);
            if(dummynode->next == NULL || dummynode->next->next == NULL)return head;
            ListNode* pre = NULL;
            ListNode* mid = dummynode->next;
            ListNode* tail = dummynode->next->next;
            while(1){
                mid->next =  pre;
                if(tail == NULL)break;
                pre = mid;
                mid = tail;
                tail = tail->next;
            }
            return mid;
        }
    };

  2. 递归法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    class Solution {
    public:
        ListNode* reverseList(ListNode* head) {
            if (!head || !head->next) {
                return head;
            }
            ListNode* newHead = reverseList(head->next);

            head->next->next = head;     //下一个结点指回自己
            head->next = NULL;
            return newHead;
        }
    };

力扣92 反转链表 II

算法思路

该题难点在于要求一次遍历，需要理清变量的位置。

哨兵节点：dummynode

反转链表需要三个变量：fir、sec、thr

确定反转后的头和尾需要两个变量：pre、tail

3

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        if(!head)return NULL;
        if(!head->next)return head;
        if(m == n)return head;
        ListNode* dummynode = new ListNode(0,head);
        ListNode* fir = dummynode;
        ListNode* sec = dummynode->next;
        ListNode* thr = dummynode->next->next;
        ListNode* pre;//连接m点
        ListNode* tail;//连接n点

        while(thr){
            if(m == 1)break;
            fir = sec;
            sec = thr;
            thr = thr->next;
            n--;
            m--;
        }
        pre = fir;
        tail = sec;
        while(thr){
            fir= sec;
            sec = thr;
            thr = thr->next;
            sec->next = fir;
            n--;
            if(n == 1)break;
        }
        tail->next = thr;
        pre->next = sec;
        return dummynode->next;
    }
};

力扣25 K 个一组翻转链表

算法思路

  1. 遍历一遍链表，获得链表长度cnt，根据cnt分割出每段len
  2. 用三指针进行反转

与上题类似。可以继续沿用上题的我画的图

！！！注意注意！！！花了半个小时debug，问题在于 fir = tail;反转一段链表后，需要更新fir为tail

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        if(!head)return NULL;
        if(!head->next)return head;
        ListNode* dummynode = new ListNode(0,head);
        //得到长度
        ListNode* cur = dummynode;
        int cnt = 0;
        while(cur){
            cnt++;
            cur = cur->next;
        }
        cnt--;
        int len = cnt/k;
        ListNode* fir = dummynode;
        ListNode* sec = dummynode->next;
        ListNode* thr = dummynode->next->next;
        ListNode* pre;
        ListNode* tail;
        for(int i = 0 ; i < len; i ++){
            pre = fir;
            tail = sec;
            for(int j = 0; j < k; j ++){
                sec->next = fir;
                fir = sec;
                sec = thr;
                if(thr == NULL) thr = NULL;
                else thr = thr->next;
            }
            pre->next = fir;
            tail->next = sec;
            fir = tail;
        }
        return dummynode->next;
    }
};

思考：如何只用一次遍历。太累了，以后再解决吧。

力扣21 合并两个有序链表

力扣2 两数相加

力扣445 两数相加 II

算法思路

  1. 由于需要逆序处理链表，从个位开始相加，所以可以考虑使用栈
  2. 引入一个carry变量作为进位

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        stack<int> s1;
        stack<int> s2;
        ListNode* cur;
        //遍历l1
        cur = l1;
        while(cur){
            s1.push(cur->val);
            cur = cur->next;
        }
        //遍历l2
        cur = l2;
        while(cur){
            s2.push(cur->val);
            cur = cur->next;
        }
        ListNode* ans = NULL;
        int carry = 0;
        //当l1为空，l2为空，carry为0时结束循环
        while(!s1.empty()|| !s2.empty() || carry){
            int left = 0;
            int right = 0;
            if(!s1.empty()){
                left = s1.top();
                s1.pop() ;
            }
            if(!s2.empty()){
                right = s2.top();
                s2.pop();
            }
            int newval = left+right+carry;
            carry = newval/10;
            newval = newval%10;
            ListNode* node = new ListNode(newval);
            node->next = ans;
            ans = node;
        }
        return ans;
    }
};

力扣23 合并K个升序链表

算法思路一、

一种想法是将所有结点打散，存在一个优先队列中。但是耗时较长

image-20210126192802293

但是，可以直接的考虑应该是每次取出各个链表的第一个元素，放入优先队列。

学习优先队列的使用方法，熟悉for(auto node : lists){}这种遍历方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    struct Status {
        int val;
        ListNode *ptr;
        bool operator < (const Status &rhs) const {
            return val > rhs.val;
        }
    };
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        priority_queue<Status> q;
        for (auto node: lists) {
            if (node) q.push({node->val, node});
        }
        ListNode* dummynode = new ListNode(0);
        ListNode* tail = dummynode;
        while (!q.empty()) {
            auto front = q.top(); q.pop();
            tail->next = front.ptr; 
            tail = tail->next;
            if (front.ptr->next) q.push({front.ptr->next->val, front.ptr->next});
        }
        return dummynode->next;
    }
};

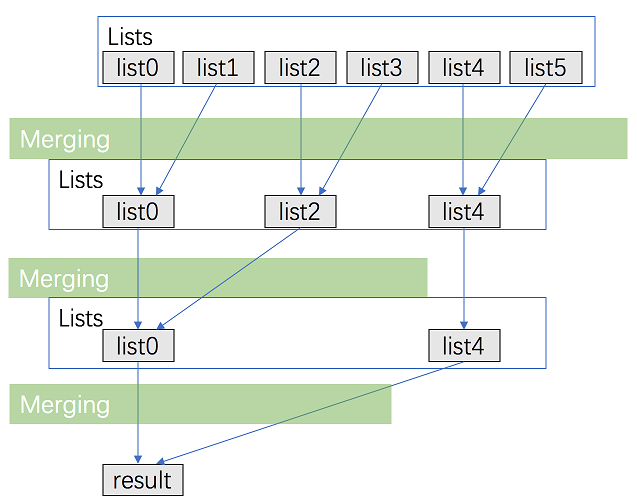
算法思路二、

分治合并。

img

需要两个函数：1.用于合并两个链表；2.分治递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    //合并两个链表
    ListNode* merge2Lists(ListNode* l1, ListNode* l2){
        if(!l1 && !l2)return NULL;
        if(!l1 )return l2;
        if(!l2) return l1;
        ListNode* cur1 = l1;
        ListNode* cur2 = l2;
        ListNode* dummynode = new ListNode(0);
        ListNode* cur = dummynode;
        while(cur1 && cur2){
            if(cur1->val < cur2->val){
                ListNode* temp = new ListNode(cur1->val);
                cur->next = temp;
                cur1 = cur1->next;
                cur = cur->next;
            }else if(cur1->val >= cur2->val){
                ListNode* temp = new ListNode(cur2->val);
                cur->next = temp;
                cur2 = cur2->next;
                cur = cur->next;
            }
        }
        cur->next = cur1? cur1 : cur2;
        return dummynode->next;
    }
    //递归
    ListNode* fun(vector<ListNode*>& lists, int left, int right){
        int mid = (left + right)/2;
        if(left == right)return lists[left];
        if(left > right)return NULL;
        ListNode* ans = merge2Lists(fun(lists, left, mid),fun(lists, mid+1, right));
        return ans;
    }
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return fun(lists, 0, lists.size()-1);
    }
};

链表暂告一段落......

数组相关

力扣485 最大连续1的个数

力扣495 提莫攻击

力扣414 第三大的数

力扣 剑指 Offer 40. 最小的k个数

力扣628 三个数的最大乘积

力扣645 错误的集合

https://leetcode-cn.com/problems/set-mismatch/solution/cyi-huo-fa-xiang-jie-by-feng-feng-19/

力扣697 数组的度

算法思路

  1. 构建一个unordered_map<int,pair<int,int>>，其中pair包含数据出现次数与数据第一次出现的坐标

力扣448 找到所有数组中消失的数字

动态规划相关

image-20210203195708610

动态规划组成部分：

  1. 确定状态：最后一步和子问题

    image-20210203200248268

  2. 转移方程

    image-20210203200631362

  3. 初始条件和边界情况

    image-20210203201010114

  4. 计算顺序（递归：自顶向下，动态规划：自底向上）

    image-20210203201219009
image-20210203203659002

力扣338 比特位计数

算法思路

要输出二进制数的‘1’的个数，只需要考虑两种情况：

  1. 奇数：\(f(i) = f(i-1)+1\)
  2. 偶数：\(f(i) = f(i/2)\)

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> countBits(int num) {
        vector<int> ans;
        if(num >= 0)ans.push_back(0);
        if(num >= 1)ans.push_back(1);
        for(int i = 2; i <= num; i ++){
            if(i%2 == 1){
                ans.push_back(ans[i-1]+1);
            }else{
                ans.push_back(ans[i/2]);
            }
        }
        return ans;
    }
};

力扣45 跳跃游戏 II

第一种思路使用动态规划：

另开数组记录每一个位置的步数，然后\(f(x) = min({f(0),f(1),...f(x-1)})+1\)

时间复杂度为\(O(n^2)\)

第二种思路，从后往前

最坏时间复杂度也为\(O(n^2)\)，超出时间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int jump(vector<int>& nums) {
        int pos = nums.size()-1;
        int ans = 0;
        while(pos!=0){
            for(int i = 0; i < pos; i ++){
                if(nums[i]+i >= pos){
                    pos = i;
                    ans ++;
                    break;
                }
            }
        }
        return ans;
    }
};

第三种思路，贪心算法

时间复杂度为\(O(n)\)

在2的后面的两个数之中，找出一个能到达最远位置的数

image.png

在3的后面的三个数之中，找出一个能到达最远位置的数

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int jump(vector<int>& nums) {
        int ans = 0;
        int end = 0;
        int maxpos = 0;
        for(int i = 0; i < nums.size()-1; i ++){
            maxpos = max(maxpos,nums[i]+i);
            if(i == end){
                end = maxpos;
                ans++;
            }
        }
        return ans;
    }
};

力扣198 打家劫舍

算法思路

转移方程：\(f(i) = max(f(i-1),f(i-2)+nums[i])\)

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size() == 0)return 0;
        int size = nums.size();
        int arr[size];
        if(size >= 1)arr[0] = nums[0];
        if(size >= 2)arr[1] = max(nums[0],nums[1]);
        for(int i = 2; i < size; i ++){
            arr[i] = max(arr[i-1],arr[i-2]+nums[i]);
        }

        return arr[size-1];
    }
};

优化方案：发现可将上面的arr和nums合并为一个数组

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size() == 0)return 0;
        if(nums.size() >= 2)nums[1] = max(nums[0],nums[1]);
        for(int i = 2; i < nums.size(); i ++){
            nums[i] = max(nums[i-1],nums[i-2]+nums[i]);
        }

        return nums[nums.size()-1];
    }
};

力扣213 打家劫舍 II

算法思路

  1. 分为两种情况：（1）算头不算尾；（2）算尾不算头
  2. 在上述两种情况下，进行“打家劫舍”的操作

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int first_rob(vector<int> & nums){
    if(nums.size() >= 2)nums[1] = max(nums[0],nums[1]);
    for(int i = 2; i < nums.size(); i ++){
        nums[i] = max(nums[i-1], nums[i-2]+nums[i]);
    }
    return nums[nums.size()-1];
}
int rob(vector<int>& nums) {
    //分为两种情况，调用first_rob函数
    if(nums.size()==0)return 0;
    if(nums.size() == 1)return nums[0];
    vector<int>::const_iterator head = nums.begin();
    vector<int>::const_iterator tail = nums.begin()+nums.size();
    vector<int> x(head+1, tail);
    vector<int> y(head, tail-1);
    return max(first_rob(x), first_rob(y));
}

力扣650 只有两个键的键盘

算法思路：DP

  1. 寻找最大的因子j
  2. 状态转移方程为\(f(i) = f(j) + i/j\)

该算法效率不高，因为额外计算了很多不必要的量，最坏情况时间复杂度为\(O(n^2)\)

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int minSteps(int n) {
    int arr[n+1];
    if(n >= 0)arr[0] = 0;
    if(n >= 1)arr[1] = 0;
    if(n >= 2)arr[2] = 2;
    for(int i = 3; i <= n; i ++){
        for(int j = i/2+1; j >0; j --){
            if(i%j == 0){
                arr[i] = arr[j] + i/j;
                break;
            }
        }

    }
    return arr[n];
}

算法思路二：递归法

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int minSteps(int n) {
        if(n == 1)return 0;
        for(int i = n/2; i > 1; i--){
            if(n%i == 0){    //得到最大因数
                return minSteps(i)+n/i;    
            }
        }
        //如果n为素数，则直接返回其本身。
        return n;
    }
};
#数据结构与算法
寒假力扣日志
https://wuhlan3.github.io/2021/01/23/寒假力扣日志/
Author
Wuhlan3
Posted on
January 23, 2021
Licensed under